
 |
Intermediate Macroeconomics | |
10. Consumption |
So far in this course we have looked at the macroeconomy and considered how the different pieces fit together. In this chapter we zero in on one of the big pieces -- household consumption expenditures. There are two reasons to focus on consumption. First, consumption expenditures make up about 70 percent of total spending in the U.S. economy. Second, the behavior of the macroeconomic models we have studied are largely driven by consumption behavior. For example, the multiplier effect in the Keynesian model in which a small change in fiscal policy can lean to a large change in national income is largely driven by consumption.
We start this chapter by reviewing the characteristics of the Keynesian consumption function that we described in an earlier chapter. The Keynesian consumption function is then compared with recent economic trends to see if the theory and the economy are consistent. We will find a few problems. We will then describe the two basic modern theories of household consumption, the life-cycle hypothesis and permanent income theory, to see what enlightenment they might provide.
![]()
In the Keynesian consumption function current disposable income is the only determinant of consumption, as shown in equation (1).
| C(t) = C0 + c * Y(t) | (1) |
Note: the (t) represents a specific time period. For example C(1996) and Y(1996) represent consumption and income in 1996. C(t) and C(t-1) would represent consumption this year (t) and last year (t-1).
The income induced part of consumption is critical to the Keynesian model. As income increases consumption rises by a constant fraction of that increase. The change in consumption for every $1 change in income is called the marginal propensity to consume, or MPC. If the MPC is 0.8, a $1 increase in income raises consumption by $0.80. A $1,000 increase in income raises consumption by $800.
| MPC | = change in consumption = change in income | dC(t) dY(t) |
| Marginal propensity to consume - the amount that consumption changes in response to an incremental change in disposable income. It is found by dividing the change in consumption by the change in disposable income that produced the consumption change. |
We can use some simple calculus to show that the MPC is equal to the coefficient c in the consumption equation, which is constant. Take the derivative of the consumption function with respect to income and we get the marginal propensity to consume out of income:
| MPC | = dC(t) = c dY(t) |
The key characteristics of the marginal propensity to consume is that it is constant and less than one. No matter what the level of income, a $1 increase in income always leads to a $c increase in consumption expenditures. The increase in consumption expenditures must not be more than the corresponding increase in income.
There is a second important implication of the Keynesian consumption function. The average propensity to consume, which is total consumption divided by total income, declines as income increases.
| APC | = total consumption = total income |
C(t) Y(t) |
| Average propensity to consume - the average amount of total household income that is devoted consumption expenditures. It is found by dividing total consumption by total disposable income. |
We can demonstrate the declining characteristic of the average propensity to consume again with some simple calculus. First we define the average propensity to consume as total consumption divided by total income:
| APC = | C(t) Y(t) |
Second, we substitute the Keynesian consumption function into the numerator of the definition of the average propensity to consume:
| APC = | C0 + c * Y(t) Y(t) |
Third, we divide both terms on the right-hand side of the equation by Y(t):
| APC = | C0 + c Y(t) |
Finally, take the derivative of the average propensity to consume with respect to income, d(APC)/dY,
| d(APC) d(Y) |
= - C0
Y(t)2 |
< 0 |
The derivative is always negative, which indicates that the average propensity to consume is not constant but that it gets smaller as income increases. As income, Y(t), increases then C0 / Y(t) get smaller
We can also demonstrate that the average propensity to consume declines with income with an example using the Keynesian consumption function. Assume that C(t) = 500 + 0.9 Y(t):
| Income, Y(t) | |||
| $1,000 | $10,000 | $100,000 | |
| C(t) = 500 + 0.9 Y(t) | $500 + $900 = $1,400 | $500 + $9,000 = $9,500 | $500 + $90,000 = $90,500 |
| APC = C(t) / Y(t) | 1.4 | 0.95 | 0.905 |
As income increases from $1,000 to $10,000 to $1000,000, the average propensity to consume declines from 1.4 to 0.95 to 0.905. The decline is fastest at low incomes and then slows as income grows. A simple explanation is that purchasing necessities (i.e., the autonomous consumption, C0 part of the Keynesian consumption function) consumes a smaller proportion of income as income increases.
![]()
We have described two important theoretical predictions of the Keynesian model. First, the marginal propensity to consume is constant and, second, the average propensity to consume declines as income increases. The fun of economics is having theoretical predictions that we can test using actual economic data (OK, that might not be your idea of fun, but keep that to yourself). We can test the Keynesian theory of consumption by examining the relationship between consumption and income both for a cross section of households and also over time.
We can calculate marginal and average propensities to consume by examining reported household consumption at different levels of household income. For example, let's assume one household with an annual income of $10,000 spends $12,000 per year. Obviously this household is either withdrawing money from savings or borrowing money to finance their spending, which exceeds their income by $2,000 a year. Now assume a second household with $20,000 a year income spends $18,000. The marginal and average propensities to consume given these two households can easily be calculated:
The marginal propensity to consume is calculated as the increase in spending divided by the increase in income. Spending between our two households increases by $6,000 (from $12,000 to $18,000) while income increases by $10,000 (from $10,000 to $20,000). The marginal propensity to consume is 0.60 ($6,000 spending increase divided by $10,000 income increase). For every $1.00 increase in income, spending increases by $0.60. The marginal propensity to consume is assumed to be constant over the full range of income
The average propensity to consume is calculated as total consumption divided by total income for each household. The average propensity to consume for the first household is 1.20 ($12,000 spending divided by $10,000 income). The average propensity to consume for the second household is 0.90 ($18,000 spending divided by $20,000 income). The average propensity to consume declines as income increases.
How well does our simple example match the real world. The U.S. Bureau of Labor Statistics (BLS) reports consumption expenditures for different levels of income in their Consumption Expenditure Survey. The BLS reports average consumption expenditures for 10 groups (deciles) of households with increasing average income. Figure 10-1 shows the relationship between expenditures and income for 2002.
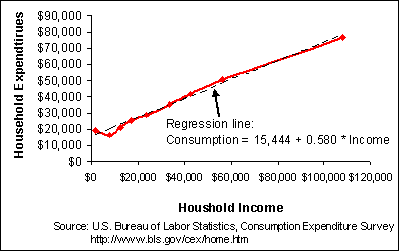
Figure 10-1 supports the simple Keynesian consumption function. The marginal propensity to consume is the slope of the graph line and appears close to a straight line. A straight line implies the marginal propensity to consume is constant. The estimated straight line (calculated using ordinary least squares regression analysis) indicates the marginal propensity to consume is about 0.58. A $1 increase in income increases consumption expenditures by $0.58 at any given level of income.
The average propensity to consume decreases as income grows. The large intercept for the straight regression line, $15,444, also implies the average propensity to consume declines as income increases as we discussed above. Figure 10-2 illustrates how the average propensity to consume declines very rapidly at low incomes, but continues to decline even as incomes grow large.
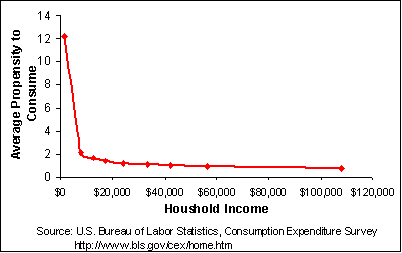
Both the estimated constant marginal propensity to consume and declining average propensity to consume are consistent with the simple Keynesian consumption function.
We can also estimate the marginal and average propensities to consume from a time series. As income grows over time consumption also grows. The change in consumption from one year to the next divided by the change in income is the marginal propensity to consume. Total consumption divided by total income in any given year is the average propensity to consume. Here is where we run into a problem.
Simon Kuznets was perhaps the first to recognize that the time series behavior of consumption does not conform to the simple Keynesian consumption function (National Product Since 1989, National Bureau of Economic Research, 1946). What is now called "Kuznets' puzzle" is the simple observation that as income increases over time the average propensity to consume does not decline.
Figure 10-3 illustrates the relationship between nominal consumption expenditures and personal disposable income over the last 50 years. The straight line relationship implies that the marginal propensity to consume is constant at about 0.93. A $1.00 increase in income from one year to the next results in an increase in consumption spending of $0.93. This is again consistent with the Keynesian model, although the estimated marginal propensity to consume in this time series (0.93) is very different from that calculated in the cross section sample above (0.58). This is an annoying difference but possibly one we could explain away.
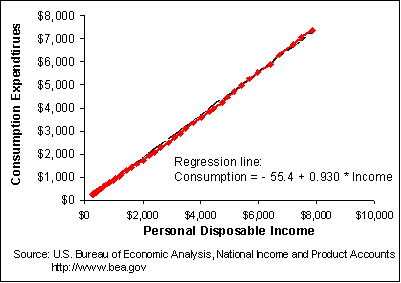
The greater problem revealed in Figure 10-3 is the very small value of the intercept. The $55.4 billion is hardly different from zero, at least when you are talking about $7,000 billion in total consumption. The regression line appears to hit close to if not on the origin (if income equals zero then consumption equals zero). The small intercept implies that the average propensity to consume is constant. Figure 10-4 presents a plot of calculated average propensities to consume at the different levels of income from the last 50 years. The average propensity to consume has not been declining as the simple Keynesian consumption function suggests it should. Over the last 50 years we might say the average propensity to consume has been constant at about 0.90, at first declining and then increasing.
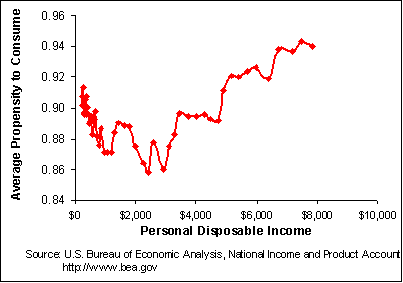
The contradiction between the time series data and the Keynesian consumption function creates a problem for our macroeconomic models. How can we use Keynes' consumption function to evaluate economic performance over time when the largest component of GDP, consumption, does not behave as predicted? Kuznets puzzle stimulated research in the 1950s on consumption theory. In the following sections we will present two dominant theories that surfaced: Franco Modigliani's life-cycle hypothesis and Milton Friedman's permanent income hypothesis.
![]()
The Keynesian consumption function assumes that current period consumption depends only on current period income. A temporary decline in income because of illness, unemployment, or recession must be met by a similar temporary decline in consumption expenditures. The life-cycle hypothesis, on the other hand, suggests that expected future income also influences current consumption. If the income decline is expected to be temporary I need not drastically reduce my consumption expenditures. I could withdraw savings to be replenished later when my income recovers. I could also borrow against my future income. Thus, current period consumption depends not only on current period income but also expected future income.
| Life-cycle hypothesis - a theory that attempts to explain how people split their income between spending and saving over their lifetimes. |
The life-cycle hypothesis was developed by Franco Modigliani and his collaborators Albert Ando and Richard Brumberg (Modiglian and Brumberg, "Utility Analysis and the Consumption Function: An Interpretation of Cross-Section data," in Post-Keynesian Economics, ed. Kenneth K. Kurihara, 1954, 388-436, and Ando and Modigliani, "The Life Cycle Hypothesis of Saving: Aggregate Implications and Tests," American Economic Review, 53, March 1963, 55-84.)
There are two fundamental assumptions made by the life-cycle hypothesis. The first assumption is that people have some expectation about their lifetime earnings. This probably strikes you as a pretty strong assumption. Have you estimated what income you will be making 10 years or 20 years from now? Perhaps we shouldn't take this assumption too literally. What if I simply asked if you expect to have a greater real income in the future than you do today. With an expectation of more future income you may be willing to go into debt today expecting to be able to pay it off in the future. While you may not be able to say what your future income will be you nevertheless act as if you could. What the life-cycle hypothesis suggests is that people make decisions about consumption today based on some expectation of future income.
The second assumption is that people maximize their utility by maintaining a steady level of consumption. A person that lives modestly for two years in a row will be much happier than another person who feasts one year and then starves the next.
Given these two assumptions we can create a model that generates certain implications regarding the marginal and average propensities to consume. The question is does this model do a better job explaining the marginal and average propensities to consume that we observe in cross-section and time series data than the Keynesian consumption function? The answer is yes.
The consumption smoothing assumption implies that people prefer to consume the same amount every year. Your expected lifetime consumption equals the average yearly consumption times your life expectancy:
| Lifetime consumption = C * NL | (2) |
Your lifetime income is equal to any current wealth you may have plus the total of you expected future earnings. To simplify our model we will simply suggest that future earning are constant so that total future earnings equals average annual income times the number of years you will work. We could add a slight complication in terms of bequests you may want to leave you family at your death but this would not affect the results of our analysis.
| Lifetime income = WR + WL * YL | (3) |
The often annoying rule of accounting in equation (4) requires that total lifetime consumption, equation (2), must equal total lifetime earnings, equation (3).
| C * NL = WR + WL * YL | (4) |
If we divide the accounting identity through by the number of years we expect to live, NL, we obtain the average annual level of consumption.
| Average annual consumption = C = | 1 * WR + WL * YL
NL NL |
The first result of this model is that the marginal propensity to consume (MPC) depends on whether a change in income is expected to be temporary or permanent. First, consider a temporary change in current income, which can considered equivalent to a change in current wealth, WR. Take the derivative of average annual consumption, equation (4), with respect to initial wealth, WR, and we get the marginal propensity to consume out of a temporary change in income. The marginal propensity to consume out of a temporary change in income is equal to the change in current year consumption divided by the change in wealth (i.e., the temporary change in current period income):
| Marginal Propensity to Consume (MPC) out of current wealth = | dC = dWR |
1 NL |
Consider a simple example. Assume Congress passes a one-time tax rebate bill. You get a $1,000 check in the mail. If you desire to smooth consumption you should spend only a small portion of the $1,000 every year for the rest of your life. If you expect to live for another 20 years consumption smoothing implies you will spend only an additional $50 a year ($1,000 divided by 20 years). The marginal propensity to consume out of a temporary change in income will always be equal to 1 divided by the number of years you expect to live.
Now consider a permanent change in income. Let's say you obtain your college degree so that your future income in all years now increases by some amount. Your total lifetime earning increases by the permanent increase in your income times the number of years you will be working. Consumption smoothing implies that you will spread that total increase in income over your lifetime. Take the derivative of average annual consumption, equation (4), with respect to average annual income, YL, and we get the marginal propensity to consume out of a permanent change in income. The marginal propensity to consume out of a permanent change in income is always the number of years of labor divided by the number of years you expect to live.
| Marginal Propensity to Consume (MPC) out of permanent income = | dC = dY |
WL NL |
A temporary change in income is spread out over your entire lifetime so that the immediate change in consumption is small: the change in income divided by your expected lifespan. A permanent change in income, on the other hand allows a larger change in current consumption: the change in income times the number of years you expect to work divided by your expected lifespan.
We can illustrate the implications of the life-cycle model using a simple numerical model. Assume you live for 6 periods (e.g., decades). During the first four periods you earn income and during the last two periods you are retired. Your best plan is to maintain a steady level of consumption over all six periods. To do this you must save during the first four periods and live off those savings during the last two.
Base Case. We start with a base case. We earn $15 per period for 4 periods. Total expected lifetime income is $60. Since we want to maintain a steady level of consumption we divide total expected lifetime income by the number of periods we expect to live. Consumption each period will total $10 ($60 total lifetime income divided by 6 periods). Savings during the first four periods of $5 each period ($15 income less $10 consumption) supports continuing consumption during the last two periods.
| Period | 1 | 2 | 3 | 4 | 5 | 6 | Total |
| Income, Y | 15 | 15 | 15 | 15 | 0 | 0 | 60 |
| Consumption, C | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| Savings per period | 5 | 5 | 5 | 5 | -10 | -10 | 0 |
We can calculate the average propensity to consume (APC) for period 1 as total period 1 consumption ($10) divided by total period 1 income ($15):
| APC (period 1) = | Consumption (period 1) = Income (period 1) |
10 = 0.67 15 |
Case 1. Let's consider what happens if there is a temporary (period 1 only) increase in income of $30 (from $15 to $45). Total lifetime income increases to $90 and consumption each period is now $15 ($90 divided by 6 periods).
| Period | 1 | 2 | 3 | 4 | 5 | 6 | Total |
| Income, Y | 45 | 15 | 15 | 15 | 0 | 0 | 90 |
| Consumption, C | 15 | 15 | 15 | 15 | 15 | 15 | 90 |
We can calculate the marginal propensity to consume from the change in consumption in period 1 between the base case and case 1 by dividing the change in income in period 1 between the base case and case 1. The temporary increase in income in period 1 of $30 ($15 to $45) leads to an increase in consumption of $5 (from $10 to $15). The marginal propensity to consume in period 1 is 0.17 ($5/$30), which is equal to 1 divided by the number of periods left in the person's lifetime.
| MPC (period 1) = | change in consumption (period 1) = change in income (period 1) |
(15 - 10) = (45 - 15) |
5 = 0.17 30 |
The average propensity to consume is smaller in case 1 than the base case:
| APC (period 1) = | Consumption (period 1) = Income (period 1) |
15 = 0.33 45 |
Case 2. Now assume the increase in income is expected to be permanent.
| Period | 1 | 2 | 3 | 4 | 5 | 6 | Total |
| Income, YL | 45 | 45 | 45 | 45 | 0 | 0 | 180 |
| Consumption, C | 30 | 30 | 30 | 30 | 30 | 30 | 180 |
The marginal propensity to consume for case 2 is calculated as the increase in period 1 consumption over the base case divided by the increase in income between the base case and case 2. The expected permanent increase in income in period 1 of $30 ($15 to $45) leads to an increase in consumption of $20 (from $10 to $30). The marginal propensity to consume in period 1 is 0.67 ($20/$30), which is equal to the number of periods earning income divided by the number of periods left in the person's lifetime. The marginal propensity to consume in case 2 is much larger than in case 1.
| MPC (period 1) = | change in consumption (period 1) = change in income (period 1) |
(30 - 10) = (45 - 15) |
20 = 0.67 30 |
The average propensity to consume in case 2 is larger than case 1 but the same as the base case:
| APC (period 1) = | Consumption (period 1) = Income (period 1) |
30 = 0.67 45 |
Marginal propensity to consume out of income (MPC).
The MPC depends on whether the change in income is expected to be temporary (Case 1) or permanent (Case 2). The MPC for a an expected temporary change in income will be much smaller than that for an expected permanent change in income.
Considering only temporary changes in income, the MPC is constant for any given temporary change in income. You can easily confirm this by assuming a different level of temporary income change in case 1. The MPC will always be equal to 1 divided by the number of periods left in the person's lifetime.
For any given permanent change in income the MPC is also constant. Again plug in a different permanent change in income into case 2 and you will get an identical MPC. the MPC will be equal to the number of periods with income divided by the number of periods left in the person's lifetime.
Average propensity to consume out of income (APC).
The APC also depends on whether the expected change in income is temporary or permanent. The APC for a an expected temporary change in income will be much smaller than that for an expected permanent change in income.
We can summarize the results of the empirical studies and life-cycle model in a table that hints at how one relates to the other.
| Marginal Propensity to Consume |
Average Propensity to Consume | |
| Empirical studies: | ||
| Cross section | constant | declines with income |
| Time series | constant | constant |
| Life-cycle hypothesis: | ||
| Temporary income change | constant | declines with income |
| Permanent income change | constant | constant |
Cross Section Analysis: The relationship between consumption and increasing household income at a single point in time is characterized by differences in temporary changes in income. The highest income brackets may be expected to contain the largest proportion of households whose current income is temporarily above the accustomed level, and vice versa for the lowest income brackets.
Time Series Analysis: The relationship between consumption and increasing disposable income over time is characterized by changes in permanent income. In any given year, temporary increases in income in some households are offset by temporary declines in income by other households. The MPC is constant. Long-term year-to-year changes in income, which show up in the time series studies, are perceived to be permanent.
Finally, recall we observed that the marginal propensity to consume in the cross-section study was much smaller than that of the time series study. In the life-cycle model the marginal propensity to consume out of a temporary change in income is also much smaller than the marginal propensity to consume out of a permanent change in income.
![]()
The life-cycle hypothesis implicitly includes expectations because it considers expected future earnings and expected lifespan. This is a significant innovation over the Keynesian consumption function, which gives no consideration to expectations of future economic conditions. But, the life-cycle model does not address how expectations are formed and what happens when there are errors in those expectations.
There are different ways to specify how expectations are formed.
What happened last year is expected to happen this year. An example of a simple naive expectation is that the sun will rise in the East. This expectation is considered "naive" because it does not take into consideration what may have happened between yesterday and today. Perhaps an economics example may be better. If the inflation rate last year averaged 5 percent then a naive forecast would be that the inflation rate this year will also be 5 percent. This is a naive forecast because it may be obvious from changes in economic conditions from last year to now that the inflation rate will surely be higher or lower.
An important feature of this kind of expectation is that you can be consistently wrong. Let's say the inflation rate steadily increases by 1 percent a year for many years. For example, let's say inflation increases from 5 percent in year 1 to 6 percent the next year, and then from 6 to 7 percent, and then from 7 to 8 percent, and so on. At the start of year two you observed that inflation the previous year was 5 percent, and so your expectation for year two is 5 percent. You end up underpredicting inflation in year two by 1 percent. At the start of year three you predict 6 percent inflation because that was what it was in year two. You again underpredict by 1 percent. Every year you underpredict by 1 percent. You never catch on that inflation is steadily increasing and you consistently make the same error.
Your expectation never changes from some fixed value, no matter what has happened in the past. For example, let's say that the variable X is the probability that flipping an unbiased coin will come up heads. Hopefully you learned in probability class that no matter what happened on the previous flip of the coin, the probability of getting heads on the next flip is always 50%. In our inflation example a static expectation may be that the inflation rate will average 4 percent this year, and next year, and so on. This expectation never changes even if the inflation rate last year was 5 percent and all indications of a robust economy call for an even higher inflation rate this year.
You always correctly predict the future. We should go even further and say that you always perfectly predict the future. There is never even the slightest error in your forecast.
Expectations are surely more complicated than the ones above. Consider a refinement of naive expectations. Assume you have some understanding of how the economy works. From your basic model of the economy you develop an expectation based on past economic performance. But your forecast is a little wrong. Given this recent error in your forecasting model you add a partial correction to your next forecast to account for the unknown something. With adaptive expectations this period's expectation equals last period's expectation plus a weighted correction factor, a, times last period's forecast error:
An identical specification (just rearrange the right-hand side of the equation) is that your expectation is a linear combination of last period's expectation and last period's actual outcome:
There are three significant implications of this specification. First, adaptive expectations also represents a distributed lag on past outcomes. Since Et-1(Xt-1) = a * Xt-2 + (1 - a) * Et-2(Xt-2), and Et-2(Xt-2) = a * Xt-3 + (1 - a) * Et-3(Xt-3), and so on, we can substitute as follows:
An expectation of the future can be mathematically estimated as a function of all past outcomes. The most recent outcome carries the greatest weight, with progressively decreasing weights assigned to outcomes in the more distant past.
The second implication is that your expectation can still be consistently wrong. Again consider the situation that inflation is steadily increasing at 1 percent per year. Since you only partially correct for past expectations error you never fully account for the steady increase.
The third implication is that current information is not incorporated into your expectation. Let's say the Federal Reserve announces it will take actions to decrease the inflation rate by 1 percent. Since you only include past inflation rates in your expectation you don't account for the Fed's announcement.
Because of the problematic implications of adaptive expectations a theoretical foundation for rational expectations was developed. With rational expectations you correctly predict the future but with random errors.
You can be wrong but you will not be consistently wrong in one direction or the other. You don't have the systematic expectation error that you can get with adaptive expectations. Since expectations errors are costly there exist persistent unexploited profit opportunities. Thus rational agents have an incentive to weed out all systematic errors. There should be no detectable relationship between one period's forecast error and any previous periods. You do not keep making the same mistakes, you just make new mistakes.
Rational expectations also assumes that agents have a good (but not perfect) understanding of how the economy works. All available information is incorporated into the formation of expectations. An announcement by the Federal Reserve of future action will be accounted for in a person's expectation of future outcomes.
![]()
The permanent income hypothesis is an extension of life-cycle hypothesis. The permanent income model explicitly addresses how expectations are formed. Is a change in current income permanent or transitory? It depends on the history of changes in income and expectations.
Consumption is a function of expected permanent income (YP) and transitory income (YT):
The marginal propensity to consume out of long-term income, YP, is:
The marginal propensity to consume out of temporary income, YT, is:
So far this specification is identical to that of the Life-Cycle Hypothesis. The value of the marginal propensity to consume out of permanent income, c, and transitory income, d, are similar in concept to the life-cycle approach. If you expect permanent income of $10,000 over the next four years and you expect to live for 5 years, then your marginal propensity to consume out of permanent income may be 4/5, i.e., you will consume $8,000 every year for the next 5 years. If you expect a one period change in income of $10,000, then your marginal propensity to consume out of temporary income may be 1/5, i.e., you will consume $2,000 every year for the next 5 years.
The innovation in this model is the specification of how observed changes in income are attributed to permanent and transitory changes. Like adaptive expectations, your expectation of permanent income is conditioned on history. When you observe a change in current income you attribute part of that change, a, to a permanent change and the balance, (1 - a), to a temporary change. The fraction, a, is estimated from past experience regarding how much past changes in income were permanent versus transitory. Thus, expected "permanent" income is based on last year's income plus some fraction of the difference between current and last year's income:
Transitory income is:
The guts of this model is how the value of a is calculated. The methodology relates to estimation using ordinary least squares regression, but is beyond the scope of this course.
The close relationship between this model and the Life-Cycle Hypothesis means the explanations for the declining average propensity to consume (APC) in cross-section studies and constant APC in time series studies are essentially identical.
![]()
Empirical studies that have compared actual consumption behavior with the predictions of the life-cycle or permanent income hypotheses have found that consumptions appears more sensitive to changes in income than implied by the models. People who receive a temporary increase in income spend much more of it than they should. Very little is saved for future years. This result is called "excess sensitivity". A much larger change in consumption occurs for a given change in income than predicted.
There are several possible explanations:
Some durable good purchases are "lumpy". Expensive items like a car or furniture require large payments that cannot be made until a large (even temporary) increase in income is realized.
Consumption reported in the national GDP accounts and used in empirical studies does not correspond to the theoretical meaning of consumption. The purchase of a durable good (e.g., car or furniture) today is reported as consumption today in the GDP accounts, but actually represents consumption over the usable life of the product in economic theory. Thus there is less of an actual change in consumption taking place than the numbers indicate.
Imperfect credit markets (liquidity constraints). At low levels of income people cannot borrow money to maintain smooth consumption.
Consumption smoothing is not the only motive - there is also a precautionary savings motive that is not reflected in life-cycle model. A precautionary savings motive introduces additional interesting explanations of consumption that reflect uncertainty of the future (e.g., an expectation of an economic recession).
Adaptive or rational expectations do not hold. Consumers are "myopic". Any change in income is assumed to be a permanent change in income and consumption responds fully to changes in income.
![]()
Do announced temporary tax cuts or tax increases affect the economy as Keynes suggested?
Probably not.
According to the life-cycle and permanent income hypotheses the current year's change in consumption due to a temporary change in income from a tax cut or increase is small (i.e., the marginal propensity to consume and the multiplier are much smaller than Keynes believed.)
Will a tax cut financed by government borrowing stimulate total demand (another Keynesian belief)?
Maybe not
Government will someday have to pay off the debt and a future tax increase may be expected. Private savings may then increase by the full amount of the tax cut with the expectation that the savings will be required to pay off a future tax increase. We can also tell this story slightly differently. The government finances its deficit spending by selling Treasury bills. The public reduces their spending in order to buy the Treasury bills. Private savings increase by the amount of Treasury bills purchased. In the future when the government raises taxes to pay off the debt the public simply sells the Treasury bills back to the government. The bottom line is there is no change in aggregate spending. An increase in government spending is fully offset by a decrease in household spending because households lend the money to the government by buying Treasury bills.
It seems obvious that when the interest rate increases this should motivate people to increase their rate of savings. After all, the payback from savings certainly increases. Do higher interest rates lead to higher savings and lower consumption?
Maybe not.
A higher interest rate means current wealth, which is earning interest, will be worth more in the future. This is similar to an expected increase in future income. With an expected increase in future income you have an incentive to increase consumption today (remember the marginal propensity to consume out of a permanent change in income). You consume some of that additional future wealth today. Thus, a higher interest rate can lead to more consumption and less savings.
Politicians occasionally criticize the low savings rate in this country and advocate an increase in Social Security to solve the problem. Does a government Social Security program lead to higher national savings rate?
Maybe not.
If there are no liquidity constraints (i.e., you can freely borrow or save money), a higher savings rate forced by the government (Social Security) may be offset dollar-for-dollar by a reduction in personal savings. The net effect is no change in national savings. This assumes that people are able to save at the desired rate to be able to maintain consumption during retirement. If I am already saving as much as I want to to support my future consumption why would I let the government force me to increase that rate. The more the government makes me save the less I will save voluntarily. However, if private savings is somehow constrained, which is the reference to the liquidity constraint, then we could get an increase in national savings. If I am not saving as much as I would like or should because I don't have good or safe opportunities for investing my money then a government run savings program may represent a beneficial new alternative.
File last modified: April 8, 2004
© Tancred Lidderdale (Tancred@Lidderdale.com)