
 |
Intermediate Macroeconomics | |
11. Investment |
Contents
1. Introduction1. Introduction
When you hear the term investment you probably think of buying stocks or bonds. This is not what economists consider as investment in their economic models. When you buy a stock or bond you are only transferring a claim of ownership on the firm's existing assets from one person to another. You are not increasing the productive capacity or the physical assets of the firm. Investment in economic models represents the flow of spending that adds to the physical stock of real capital.
| Investment in real capital - production and accumulation of goods for future use in production processes. |
The National Income and Product Accounts (NIPA) includes these categories of investment expenditures:
Residential fixed investment - new housing that people buy to live in and landlords buy to rent out.
Change in inventories - goods in storage that will be used to produce other goods, including raw materials, work-in-process, and finished products. A decline in inventories is recorded as negative investment.
You should recognize that the traditional classification of investment excludes two important categories. First, it excludes government investment such as in roads, schools, and so on. Government spending should be handled differently since it is generally not dependent on the usual macro variables such as interest rates and aggregate demand. Moreover, government investment can behave very differently during business cycles where governments use spending as a tool of fiscal policy.
Second, it omits investment in human capital through education and training. Investment in human capital is a very important consideration in long-run economic growth models and in comparing different regions of the world. In our short-run business cycle models it is implicitly assumed that investment in human capital does not vary significantly.
Investment has always been high on the economics research agenda for many reasons. In particular:
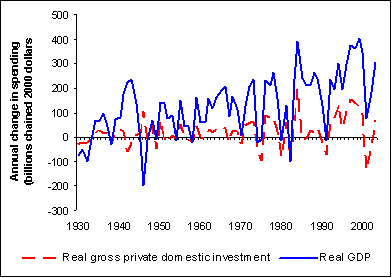
Figure 11-1. Year-to-year Changes in Real Investment and Real GDP.
Source: U.S. Dept. of Commerce, Bureau of Economic Analysis, Annual NIPA Table (http://www.bea.gov/bea/dn/home/gdp.htm)
In the short run, investment spending may be destabilizing. For example, as demand and income declines such as during a recession, firms respond by reducing investment spending, which further depresses the economy.
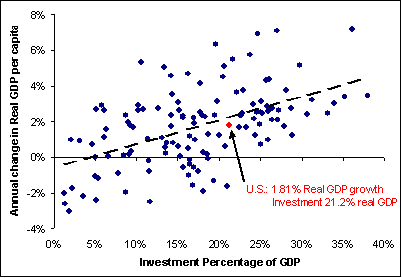
Figure 11-2. Investment and Growth.
Source: Penn World Tables 5.6 (http://datacentre.chass.utoronto.ca/pwt/index.html)
This chapter focuses on the short-run dynamics of investment. Does investment vary with the level of demand and income or is it autonomous (fixed) as in the simple Keynesian macroeconomic model? Does investment change as interest rates rise and fall?
After briefly defining investment we will cover four models of investment:
Net Present Value - this is one of the standard "Business School" approaches to how individuals compare different opportunities when making investment decisions. While it is not a model that can be directly applied to macroeconomic models it does provide insight into the relationships of investment to demand, prices and interest rates.
Simple Accelerator Model - one of the most basic macroeconomic investment models, the simple accelerator model relates investment (changes in the level of the capital stock) to changes in demand. This model of investment is frequently applied to modeling inventory behavior.
Neoclassical with Flexible Accelerator Model - a more rigorous approach to determining the desired level of capital stock and the rate of investment to reach that desired level of capital. The resulting flexible accelerator model is similar to the simple accelerator model, but adds interest rates and expected inflation to demand as explanatory variables.
q-Theory - economists don't completely ignore the stock market. One of the problems in estimating investment models and forecasting is that some variables are not directly observable. We generally know how much capital costs, but how much is capital worth? The stock market provides an indication.
Finally, we utilize these models to review the effect of government policy on desired investment.
This is not an exhaustive list of short-run investment models. There are other models of short-run changes in investment and the capital stock. Every model has its shortcomings such as possible unrealistic assumptions, behavior that the model does not address, unobservable variables, and so on. What we hope is that when you study investment behavior you are able to select the best model for the specific situation being analyzed and you recognize the restrictions imposed by the assumptions and structure of the model being used.
![]()
2. Gross Investment, Net Investment, and Depreciation
Investment is the flow of spending that adds to the physical stock of real capital. We begin the year with some level of capital and we end the year at some different level:
Int = Kt - Kt-1
where,
Int = net investment in period t
Kt = capital stock at the end of period t
Kt-1 = capital stock at the end of period t-1 (start of period t)
This simple specification ignores depreciation. Physical capital wears out and becomes obsolete. Some additional investment spending must be directed to the replacement of depreciating capital. The Commerce Department reports depreciation as "consumption of fixed capital." A common assumption is that the depreciation rate is a fixed fraction of the level of capital (capital depreciates geometrically at a constant rate), and replacement investment is:
Irt = d Kt-1
Irt = investment in replacement capital in period t
d = depreciation rate
Total gross investment is the sum of net investment and replacement investment:
Igt = Int + Irt
= Kt - Kt-1 + d Kt-1
= Kt - (1 - d) Kt-1
Igt = gross investment in period t
In the macroeconomic models of the aggregate economy we covered in earlier chapters, the measure of investment we were most interested in was gross investment because that represents total aggregate spending. The economic models of investment in this chapter, however, generally focus on net investment (and the desired level of capital). Gross investment is then equal to net investment determined from the model plus estimated depreciation such as calculated above.
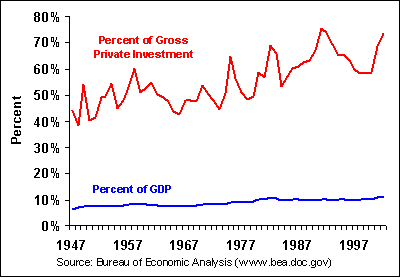
Figure 11-3. Depreciation of Gross Capital Stock.
Source: U.S. Dept. of Commerce, Bureau of Economic Analysis (http://www.bea.doc.gov/).
![]()
3. Model 1 - Net Present Value (NPV)
You have a fixed amount of funds to invest and several good investments projects to pick from. How do you choose? How do you compare an investment that pays out a large sum 3 years from now to one that has an even bigger payoff but you have to wait 6 years for it? And how do you compare those with a project that pays out a smaller sum but steadily every year?
Investment projects with very different future payoffs can be compared by expressing future income and expenses in current value terms by discounting future dollar values by the nominal interest rate.
| Discounting future income
Assume a 10% nominal (market) interest rate:
Suppose your firm offers you a choice of bonuses: $1.05 paid one year from now or $1.25 paid two years from now. Which should you take? Assume a 10% nominal interest rate and ignore time preferences (you're not desperate for cash).
The best deal is the one that provides the highest present value of discounted future income. |
The total present-day value of all current and expected future revenues and expenses is Net Present Value (NPV):
NPV = (Revenue - Expense)year 1
+ (Revenue - Expense)year 2 / (1+i)
+ (Revenue - Expense)year 3 / (1+i)(1+i)
+ ...
where, i = nominal interest rate
Let's consider a simple investment option in Table 11-2. An investment of $100 today produces revenue of $50 one year from now and $80 two years from now. Is this a profitable investment? Just because the future payoffs may be larger than today's investment doesn't necessarily mean it is profitable given the prevailing interest rate. Looks can be deceiving. You might be able to do better investing elsewhere. We can get an idea by comparing the net present value of the future payoffs to today's cost to invest.
Note: revenues, expenses, and the nominal interest rate include expected inflation. Revenues and expenses are assumed to occur at the beginning of each year (this avoids the unnecessary complicating issue of compounded interest rates).
| Table 11-2. Cash Flow vs Net Present Value of Possible Investment Projects | |||||
| Nominal interest rate = 10%
Revenues and expenses occur at the beginning of each year | |||||
| Revenue | Expense | Net Cash Flow = Revenue - Expense |
Net Present Value | ||
| Year 1 | $ 0 | $100 | - $100 | - $100 | |
| Year 2 | $50 | $ 0 | $ 50 | + $45.45 | |
| Year 3 | $80 | $ 0 | $ 80 | + $66.12 | |
| Totals | $130 | $100 | + $ 30 | + $11.57 | |
| NPV Year 1 Net Cash Flow = - $100
NPV Year 2 Net Cash Flow = + $50/1.1 = + $45.45 NPV Year 3 Net Cash Flow = + $80/(1.1)(1.1) = + $66.12 NPV = - $100 + $45.45 + $66.12 = $11.57 | |||||
In this case the NPV pf the project is positive (+$11.57), indicating that the return on this investment is greater than could be earned by depositing your money at the nominal interest rate. It is a worthwhile investment.
What would happen if the revenue projection for year 3 fell to $60. You would still have a positive total cash flow but is it still a worthwhile investment? No, because the present value of the $60 payoff two years from now (the beginning of year 3) is $49.59 and the net present value of the project is now negative (- $4.96). You could do better by depositing your money at the nominal interest rate rather than invest in the project.
Now what would happen if the nominal interest rate rises to 15%, is this still a good project (Year 3 revenues are back up to $80)? Yes, but barely with the NPV = $3.97.
Conclusion 1: As aggregate demand and projected cash flows rise or fall, the NPV of investments rise and fall. Investment should appear to be a positive function of national income and aggregate demand (higher income and demand should lead to higher investment).
Conclusion 2: As the nominal interest rate increases, the NPV should decline (if future cash flow is positive). Investment should appear to be inversely related to interest rate. A higher interest rate leads to lower investment.
Net Present Value analysis can be used by firms to evaluate potential investment projects. NPV analysis also provides some reassurance to macroeconomists that investment is positively related to income and negatively related to the interest rate. But the NPV approach does not provide a theoretical foundation for determining how much investment will be undertaken. How many potential investment projects are there? What is the pattern of their cash flows? On aggregate measures this firm-level NPV approach is silent.
![]()
4. Model 2 - Simple Accelerator Model
Our first macroeconomic model is the simple accelerator model. We assume there exists an optimum quantity of real capital for a given level of output. When demand increases firms want to hold a larger stock of capital. This capital can be nonresidential fixed investment (structures and equipment) necessary to increase production or a higher level of inventories to meet consumer demands.
If we assume:
The level of capital at the start of period t (end of period t-1) will then be:
Kt-1 = ß Yt-1
where,
Kt-1 = capital stock at the end of period t-1
Yt-1 = output last period, t-1
ß = optimal quantity of capital required to produce 1 unit of output
Similarly, the level of capital at the end of period t will be:
Kt = ß Yt
Since net investment expenditures equals the change in the level of real capital, net investment is proportional to the expected change in output:
Int = Kt - Kt-1
= ß Yt - ß Yt-1
= ß (Yt - Yt-1)
| Simple Accelerator Model - firms attempt to maintain a fixed ratio of their capital stock to expected sales. Net investment is a positive function of the change in expected output. |
Note that this is a model for net investment rather than gross investment. For gross investment this simple model must be amended to account for replacement capital. As noted earlier it is commonly assumed that replacement capital (depreciation) is a fixed fraction, d, of the capital stock, or d Kt-1. Thus, gross investment can be represented as:
Igt = Int + d Kt-1
= ß (Yt - Yt-1) + d ß Yt-1
As useful as this model is we must be aware of its limitations. For example:
The simple accelerator model assumes that the desired level of capital stock is a fixed ratio to output. But there are reasons to expect this ratio is not constant but varies depending upon the cost of capital and labor, interest rates and tax rates, etc.
The simple accelerator also assumes that firms can instantaneously adjust their capital stock to the observed level of demand. This is expecting too much. "Time-to-build" can be significant. Accelerating the installation of new factories and equipment may result in much higher costs.
We can consider these additional economic variables by constructing a more complex macroeconomic model of the desired level of the capital stock and investment -- the Neoclassical model with a flexible accelerator.
![]()
5. Model 3 - Neoclassical with Flexible Accelerator Model
The neoclassical investment model takes a more rigorous approach to estimating the desired level of capital. Building from the microeconomic model of the firm's production function and profit-maximizing behavior we can relate the desired level of capital and investment to product prices (demand) and interest rates. We also improve on the simple accelerator model by explicitly accounting for the reality that it takes time to build new plant and equipment.
First we calculate desired level of capital stock using the microeconomic firm profit maximization problem. Start with the firm's production function:
Y = f(K,L)
where,
Y = output
K = capital stock
L = labor inputs to production process
f(K,L) = production is a function of capital and labor
The marginal product of capital, MP(capital), is the increase in output resulting from the use of one more unit of capital (assuming the level of labor, L, fixed). Using simple calculus the marginal product of capital is the first-order derivative:
MP(capital) = ∂Y = ∂f(k,L)
∂K ∂K
∂Y = change in output
∂K = change in capital
For a profit maximizing firm:
Profit = p * Y - c * K - w * L
= p * f(K,L) - c * K - w * L
p = price of output
c = rental cost of capital
w = labor wage rate
Note that we specify a "rental" cost of capital (also frequently referred to as the "user" cost of capital) rather than a "purchase" price of capital. The reason will hopefully become clearer when we discuss the rental cost of capital in the next section.
The first-order conditions of the microeconomic profit maximization problem require marginal cost of using capital equal marginal benefit of using capital (see the box below for an example of the profit maximization problem using the Cobb-Douglas production function):
c = p * ∂f(K,L)
∂K
= p * MP(capital)
In equilibrium the rental cost of capital, c, equals the value of the marginal product of capital, p* df(K,L)/dK. In other words, when you increase your capital stock by 1 unit you can produce an additional ∂f(K,L)/∂K units of product, which you can sell at price p for a total revenue of p * ∂f(K,L)/∂K. If the rental cost of capital is less than the value of the output produced by using one more unit of capital then the firm should increase its level of capital.
| Marginal Product of Capital - the physical increase in output resulting from the use of one more unit of capital.
Value of the Marginal Product of Capital - the value of the physical increase in output resulting from the use of one more unit of capital (the price of output times the marginal product of capital). Rental Cost of Capital - the cost of using one more unit of capital in production. |
We must assume some specific functional form for the firm's production function to get an explicit solution for desired level of capital. In general, the desired level of capital, K*, is:
| Profit Maximization and the Cobb-Douglas Production Function
One of the favorite production functions in economics is the Cobb-Douglas production function, which is: Y = Ka Lb
K = level of capital
L = labor inputs
a, b = estimated "technology" coefficients
The profit maximization problem can be solved as follows: Profit = p * Y - c * K - w * L
= p * Ka * Lb - c * K - w * L
The first-order conditions (partial derivatives) are: ∂ Profit = a * p * Ka-1 * Lb - c = 0
∂ K
∂ Profit = b * p * Ka * Lb-1 - w = 0
∂ L
One of the solutions to the first-order conditions is: K* = a * (p/c) * Y Which simply says the desired level of capital (K*) is a function of technology (the coefficient a from the production function), the price of the product relative to the rental cost of capital (p/c), and total output (Y). |
While average product prices are observable (e.g., inflation indexes) and the marginal product of capital can be estimated, the rental cost of capital for a macroeconomy is not directly observable.
To determine the rental cost of capital we assume that firms finance the purchase of capital by borrowing money at the nominal interest rate. Let's say the firm wants to purchase a $100 piece of equipment. The firm borrows $100 at the nominal interest rate. After one year the firm could sell the equipment for $100 and pay off the loan. the cost to the firm for using (renting) the equipment for one year was just the interest paid on the $100 loan.
Even if the firm finances investment out of past profits (retained earnings) or the sale of stocks or bonds, it should still consider the nominal interest rate as the gross rental cost since it represents the opportunity cost of not loaning out those funds and earning interest on them.
The gross rental cost of capital, which equals the nominal interest rate, must be adjusted for two factors:
If the price of capital has risen because of inflation the firm may be able to sell its capital at a higher price than it paid. This would reduce the cost of the capital the firm used. The nominal interest rate minus the expected inflation rate is commonly referred to as the real interest rate.
Inventory investment, just like investment in business structures and equipment should also be sensitive to the real interest rate. When a firm holds product in inventory it gives up the interest it could have earned on the money tied up in that inventory. Inventory also appreciates in value if there is inflation. Thus, the real interest rate (the nominal interest rate less the inflation rate) represents the opportunity cost of holding inventories. As the real interest rate increases, firms should reduce inventories in order to cut costs.
If the capital suffered from wear and tear or technical obsolescence, the firm pays an additional cost when it sells its capital at a price lower than it paid. This depreciation would increase the cost of the capital the firm used.
The rental cost of capital to the firm is then the combination of these three elements:
c = i - E + d
i = nominal interest rate
E = expected rate of inflation
d = expected depreciation rate
While the nominal interest rate is observable, the expected rates of depreciation and inflation are not. Economists have never gotten too excited about depreciation rates since they appear to change very little over time. Interest has always focused on expectations of inflation.
We must assume some method by which the expectation of inflation is formed based on observable variables. There are several mathematical specifications that can be applied to economic models, such as:
For example, the Keynesian model applies static expectations to inflation (prices are "sticky"). Milton Friedman popularized adaptive expectations in the late 1950s, and rational expectations started to dominate macroeconomic models in the 1970s.
For our purposes we will simply observe that the user cost of capital, hence the desired level of capital and investment is a function of expected inflation. If the nominal interest rate is unchanged but expectations of inflation increase (i.e., the real interest rate, i - E, declines), then the user cost of capital declines.
We started this section by showing how the desired level of capital of the profit maximizing firm is a negative function of the cost of capital and a positive function of the product price, labor wage rate, productivity of capital (marginal product of capital), and demand. Our further analysis of the user cost of capital adds the nominal interest rate, expected inflation, and expected depreciation rates to the mix.
In summary, investment is:
E. Rate of Investment - Flexible Accelerator
The neoclassical model reveals desired level of capital. But, how long does it take to reach the desired level, i.e., what is rate of investment? We take an approach similar to the simple accelerator model in the previous section. But, in contrast to the simple accelerator model we assume that the adjustment to the desired level of capital is longer and more variable, hence "flexible" accelerator.
With the Flexible Accelerator Model we assume firms close only a fraction, a, of the gap between desired and current actual level of capital stock each period. We can come up with a number of reasons for the delay between the recognition of the need for new capital and its installation, such as construction time, delivery lags, adjustment costs, etc. With the flexible accelerator model net investment is:
Int = a [K* - Kt-1]
Int = planned net investment during period t
K* = desired level of capital stock
Kt-1 = current actual level of capital stock at beginning of period t (end of period t-1)
a = adjustment factor, 0 < a < 1
Any of the variables that increase the desired level of capital stock increases investment. For example, any increase in product prices (demand) or decline in the real rate of interest will raise investment spending.
![]()
6. Model 4 - Tobin's q
The neoclassical model provides insight on how to estimate the cost of capital using observable variables but provides little guidance on how to determine the benefit of using real capital. The neoclassical model assumes that the technology, or the marginal product of capital, is known. Unfortunately for economists this usually isn't the case. Nobel laureate James Tobin suggested a possible solution--use the value of capital as revealed in the stock market. If the total market value of a firm's stocks and bonds exceeds the cost of replacing all of the capital it owns, this implies the value of its capital is greater than the cost of acquiring it.
| Tobin's q - the market value of installed capital divided by the replacement cost of installed capital. |
Let's consider a simple example. First let's pick an industry whose capital is relatively long-lived so that we can ignore the complications of depreciation. Suppose company X owns 10 new Boeing airplanes that cost $50 million each. The real capital owned by company X totals $500 million. If the stock market values all of the shares outstanding for this company at $600 million, this implies the value of the airplanes is greater than their total cost. In other words, the company might purchase one more plane for $50 million and increase its stock market value by $60 million. On the other hand, if the total market value of the company is only $400 million, then adding one more plane may add only $40 million to the value of the company. If the market value of the company is greater than the cost of replacing its capital it should invest in new capital. If the market value is less than its capital replacement cost it should not invest in new equipment.
The ratio of capital's market value to its replacement cost is called Tobin's q. The incentive to invest in new real capital should be a positive function of Tobin's q. As the value of the stock market increases relative to the total stock of real capital then the rate of investment should increase.
![]()
7. Complications with Empirical Analysis
With our economic models of investment we have derived theoretical relationships between investment and the various measures of aggregate economic performance such as interest rates, output, the level of prices, and so on. These models provide hypotheses that we can test using past economic activity. For example, does the rate of investment increase when interest rates decline? Generally the theoretical relationships hold. Investment is procyclical. When the economy is booming investment increases. When the economy is in a recession investment declines.
There are, however, complications that can muddy the picture. We consider two complications, credit rationing and capacity utilization.
Credit rationing exists when firms are unable to borrow money for investment even though they are willing to pay going interest rate. Banks may impose credit rationing out of concern that the loans will not get repaid or because of credit limits imposed by the Federal Reserve. Credit rationing represents a constraint to behavior of economic agents that is not recognized by our models of free market behavior. If credit rationing increases during recessions then the rate of investment may decline even if there is no change in the interest rate.
Our models also implicitly assume that capital is 100 percent utilized. If there is a decline in demand then the desired level of capital falls. However, what we observe over the business cycle is a change in the utilization rate of existing capital. When there is a fall in demand the productive capacity of the economy does not decline with it. Capacity utilization is procyclical (manufacturing plants run at higher rates when the economy is booming and at lower rates during recessions). The actual level of capital does not necessarily correspond with the desired level of capital. We may find that investment does not vary over the business cycle with changes in demand and interest rates as implied by our models. While firms may want to be able to sell some production capacity during recessions, whom do they sell it to?
![]()
8. Policy Implications
Both monetary and fiscal policy can affect the user cost of capital through their influence on the real interest rate.
Tax policy can also influence investment demand by changing the cost of capital or the value of the marginal product of capital. For example, an investment tax credit may lower the cost of capital and a reduction in the corporate income tax may raise the value of the marginal product of capital. But tax policy can have different effects on investment demand depending on how it is implemented or how firms finance investment.
The investment tax credit is a tax provision that encourages investment. Firms may deduct a portion of their current investment spending from their income tax. This tax savings lowers the cost of capital. Investment tax credits are often considered by Congress during recessions as a stimulus to the economy.
How investment tax credits affects firms' investment decisions depends on whether the credit is expected to be temporary or permanent. Consider a one-year temporary credit versus a permanent credit. Because investment projects generally take more than one year, the permanent credit should have the greater impact on the desired level of capital stock. The temporary tax credit will apply to only part of the total project cost and thus result in a smaller reduction in the cost of capital.
While a temporary tax credit has a smaller impact of the desired level of capital it has a larger impact on current period investment spending. There is an incentive to accelerate investment spending to benefit from a temporary tax credit. Spending that would have normally taken place the second year of a multi-year project may be moved up to year one. This acceleration of spending would not be necessary with a permanent tax credit.
If the government policy objective is long-term economic growth then a permanent tax credit is probably preferred because it has the larger impact on the desired level of capital. If the government policy objective is a quick economic stimulus because the economy is in a recession then a temporary credit may yield the largest increase in current period investment spending. With a temporary tax credit, though, Congress may be gambling the future on turning the economy around today. Increased investment spending this year because of the temporary credit may come at the sacrifice of lower investment spending next year. Moreover, if the government routinely enacts investment tax credits during recessions, firms could anticipate those credits and reduce their rate of investment when the economy starts to slow down thereby accelerating the rush to the recession.
The effect of a corporate income tax on investment depends on how "profit" is defined. The U.S. corporate income tax is a tax on gross profits after interest payments and depreciation are deducted but before payments are made to equity holders (e.g., dividends paid to stockholders or retained for future investment).
The impact of a corporate income tax on investment depends on the source of the investment funds:
From borrowed funds.
Interest payments on borrowed funds are deducted before the corporate income tax is charged. The rental cost of capital (interest + depreciation) is reduced by the corporate income tax rate.
From equity (stockholder) funds (e.g., retained earnings or new stock issue).
Payments on borrowed funds are made after the corporate income tax is charged. Only the depreciation component of the rental cost of capital is deducted before income tax charged.
| Finance Investment From | ||
| Borrowed Funds | Equity Funds | |
| + Revenue from product sales | + Revenue from product sales | |
| - Raw material and labor costs | - Raw material and labor costs | |
| - Depreciation | - Depreciation | |
| - Interest payments on borrowed funds | ||
| = Gross profit | = Gross profit | |
| - Corporate income tax | - Corporate income tax | |
| = Net profit | = Net profit | |
| - Interest payments on equity funds (e.g., dividend payments) | ||
Less corporate income tax is paid on borrowed funds because interest payments are deducted from revenues before the tax is calculated. Therefore the rental cost of capital is lower with borrowed funds and the rate of investment should be higher. The impact of a change in the corporate tax rate depends on how investment is financed. Similarly, a change in the corporate tax rate may change how some investment is financed.
File last modified: April 10, 2004
© Tancred Lidderdale (Tancred@Lidderdale.com)